Hallo,

der Wert steht in deiner Tabelle. Das Problem bei der Normalverteilung ist, dass wir die Ergebnisse per Hand nicht mehr berechnen können. Das wurde mittels Näherungsverfahren getan. Um nun nicht für jede einzelnen Normalverteilung eine Tabelle anzufertigen, gibt es die Tabelle der Standardnormalverteilung und eine Transformationsformel. 

Jetzt kommt es etwas drauf an, wie deine Tabelle aussieht. Meistens wird nur die Hälfte der Standardnormalverteilung aufgeschrieben, da sie symmetrisch ist. Auf Wikipedia beispielsweise sind alle Werte von Null bis 4 ( für höhere Werte ist man so nah an 100%, das man für gewöhnlich 100% annimmt). Diese Werte haben eine Wahrscheinlichkeit zwischen 50% und 100%. 

Wie deine aussieht, müsstest du selbst einmal nachprüfen (wo sie zu finden ist steht ja in deiner Lösung). 

Du gehst jetzt jedenfalls in deine Tabelle und suchst entweder einen Wert mit der Wahrscheinlichkeit \(  0{,}05 \) oder \( 0{,}95 \).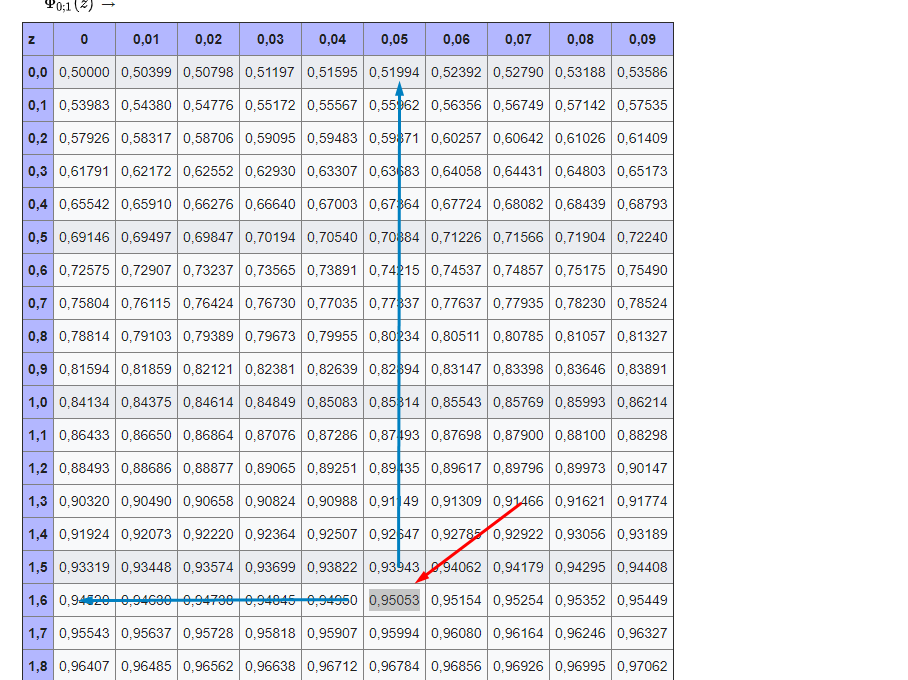

Damit erhalten wir für die Wahrscheinlichkeit \(0{,}95053 \) den Wert \(z=1{,}65 \)

Um nun die Wahrscheinlichkeit für \( 0{,}05 \) zu bestimmen, gilt

$$ \Phi(-z) = 1 - \Phi(z) $$

wir packen also einfach ein Minus davor. 

Um nun auf dein Ergebnis zu kommen, musst du wieder in deine Normalverteilun transformieren. Dazu gilt folgende Transformationsgleichung

$$ z = \frac {x - \mu} \sigma $$

\(z\) ist der Wert der Standardnormalverteilung und \( x \) der Wert der nicht Standardnormalverteilung.

Grüße Christian