Ich nehme an \(n\) ist die Raumdimension, also \(U\subseteq\mathbb{R}^n\)?
Fange damit an, zu zeigen, dass \(\partial^\alpha u\) eine Distribution ist für eine Distribution \(u\) auf \(U\). Für beliebiges, aber festes \(K\subseteq U\) musst Du geeignete \(C,N\) finden. Halte also \(K\) fest. Dann gibt es \(C_1,N_1\) für \(u\), so dass die Bedingung \[\forall\varphi\in C^\infty_{\mathrm{c}}(K)\colon|u(\varphi)|\le C_1\|\varphi\|_{C^{N_1}(K)}\] erfüllt ist. Zeige jetzt mit diesen Fakten, dass \(C_2,N_2\) existieren, so dass \[\forall\varphi\in C^\infty_{\mathrm{c}}(K)\colon|\partial^\alpha u(\varphi)|\le C_2\|\varphi\|_{C^{N_2}(K)}\] erfüllt ist.
Schreibe das mal auf; es ergibt sich ganz von alleine, was zu tun ist. Du musst nur die Definition von \(\partial^\alpha u\) einsetzen.
Lehrer/Professor, Punkte: 4K

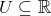 offen . Eine lineare Abbildung
offen . Eine lineare Abbildung 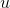 eine Distribution auf
eine Distribution auf 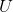 , so definieren wir für alle
, so definieren wir für alle 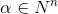 die Ableitung
die Ableitung 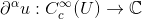 via
via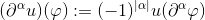 für alle
für alle 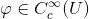 .
.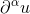 wieder eine Distribution ist und berechnen sie jeweils die Ableitung der Distribution
wieder eine Distribution ist und berechnen sie jeweils die Ableitung der Distribution 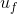 auf
auf 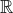 für
für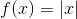 und \( f=1_{\mathbb{R}\geq0} \)
und \( f=1_{\mathbb{R}\geq0} \)