Diesen Artikel hatte ich letztens mal gelesen: 

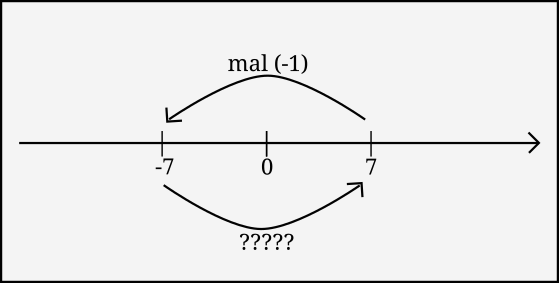
Dass Minus mal Minus gleich Plus ergibt, also z.B. (−1)∗(−1)=1(−1)∗(−1)=1 , hat keine tiefgründige Erklärung, sondern ist einfach eine DEFINITION.

Die Frage ist jetzt natürlich, warum man dies so definiert, d.h. die wirkliche Frage lautet: Warum DEFINIERT man, dass Minus mal Minus gleich Plus ergibt?

Und die Antwort darauf lautet: Dadurch werden in der Mathematik einige Dinge einfacher:

Beispiel 1: allgemeines Distributivgesetz

Nur mit der Definition, dass Minus mal Minus gleich Plus ergibt, gilt das allgemeine Distributivgesetz:

Sind aa und bb positive reelle Zahlen, so ist (a+(−a))∗(−b)=0(a+(−a))∗(−b)=0 . Will man nun hier das Distributivgesetz anwenden, muss man sich damit beschäftigen, wie man sinnvoll die Multiplikation zweier negativer Zahlen definiert. (−a)∗(−b)(−a)∗(−b) sollte ja dann so definiert werden, dass a∗(−b)+(−a)∗(−b)=0a∗(−b)+(−a)∗(−b)=0 gilt und daraus sieht man sofort, dass man (−a)∗(−b)(−a)∗(−b) als a∗ba∗b definieren sollte :)

Wozu benötigen wir das allgemeine Distributivgesetz?

Wir können z.B. nun leicht nachrechnen, dass (x−1)∗(x−2)(x−1)∗(x−2) die gleiche Funktion darstellt wie x2−3x+2x2−3x+2 .
Dies hat auch Vorteile für Leute, die nicht an der Multiplikation zweier negativer Zahlen interessiert sind, denn: Für x>=1x>=1 kommen in den obigen Ausdrücken keine Multiplikationen zweier negativer Zahlen vor. Diese Leute könnten dann zumindest leicht zeigen, dass beide Funktionen für x>=1x>=1 gleich sind. Allerdings wären sie halt dann noch zusätzlich der Meinung, dass die erste Funktion nur für x>=1x>=1 definiert ist und die zweite Funktion für x>=0x>=0 .

Beispiel 2 (erfordert Wissen über die Polynomdivision, Schüler müssen sich daher eventuell mit dem Beispiel 1 zufrieden geben ;-)): Hilfe bei der Auflösung von Gleichungen

Nehmen wir z.B. die Gleichung x2−9x−10x2−9x−10 . Dadurch, dass wir definiert haben, wie man zwei negative Zahlen miteinander multipliziert, nämlich nach der Regel “Minus mal Minus gleich Plus”, ist nun plötzlich −1−1 eine Nullstelle des obigen Polynoms und mit Hilfe der Polynomdivision können wir nun den Term (x+1)(x+1) “abspalten” und erhalten: x2−9x−10=(x+1)∗(x−10)x2−9x−10=(x+1)∗(x−10) , und siehe da, wir wissen nun auch, dass 1010 eine weitere Nullstelle ist.
Dass 1010 eine Nullstelle ist, interessiert nun auch diejenigen Leute, die sich nicht für die Multiplikation zweier negativer Zahlen interessieren, denn wenn man die 1010 oben einsetzt, kommt an keiner Stelle die Multiplikation zweier negativer Zahlen vor.
Übrigens beruht auch schon die Polynomdivision oftmals darauf, dass man zwei negative Zahlen miteinander multiplizieren kann, denn ansonsten wären beispielweise die zwei oben vorkommenden Funktionen x2−9x−10x2−9x−10 und (x+1)∗(x−10)(x+1)∗(x−10) beispielweise im Fall x=−1x=−1 für die zweite, aber nicht für die erste Funktion definiert, d.h. man könnte den Vergleich der beiden Funktionen nicht für alle xx nutzen. Für Werte von xx für die in beiden Funktionen die Multiplikation zweier negativer Zahlen vorkommt, wäre dies vielleicht nicht weiter schlimm, aber, wenn zumindest in einer dies nicht vorkommt, hat man ein Problem, auch wenn man sich wie gesagt nicht dafür interessieren würde, wie man zwei negative Zahlen miteinander multiplizieren kann.

Wie ist man auf die Definition “Minus mal Minus gleich Plus” gekommen?
Es ist, soweit ich weiß, nicht bekannt, wer zum ersten mal diese Definition angegeben hat, es kann jedoch gut sein, dass mehrere etwa zur gleichen Zeit oder zeitlich versetzt, ohne Wissen darüber, dass schon andere darauf gekommen sind, sich dies überlegt haben.
In der Mathematik hat man schon oft die Erfahrung gemacht, dass es nützlich ist, Sachen möglichst zu verallgemeinern, auch wenn man erstmal nicht weiß, wofür es gut ist, d.h. ein Beweggrund könnte gewesen sein, aus Neugierde sich zu überlegen, wie man zwei negative Zahlen miteinander multiplizieren kann (verbunden mit der Hoffnung, dass dies noch irgendwie nützlich werden könnte).
Ein anderer Grund könnte gewesen sein, dass sich die Definition einfach aufgedrängt hat, z.B. durch das Rechnen mit Variablen:
Vgl. Beispiel 1: (x−1)∗(x−2)(x−1)∗(x−2) ist, wenn man nicht definiert, wie man zwei negative Zahlen miteinander multipliziert, für x>=1x>=1 definiert, während x2−3x+2x2−3x+2 für x>=0x>=0 definiert ist.
Für x>=1x>=1 sind beide Ausdrücke identisch, daher könnte man auf die Idee kommen, dass man (x−1)∗(x−2)(x−1)∗(x−2) auch allgemein für x>=0x>=0 definieren könnte. Wenn man nun einmal naiv z.B. x=0x=0 einsetzt, erhält man (−1)∗(−2)(−1)∗(−2) , was einem zur Überlegung führen könnte, ob man nicht allgemein sinnvoll die Multiplikation zweier negativer Zahlen definieren könnte.
Was allerdings jetzt nachträglich als eine simple Idee erscheint, war alles andere als simpel und es hat eine lange Zeit gedauert, bis einer auf diese Idee gekommen ist.
Schon die Einführung von Variablen, den negativen Zahlen, etc. sind Errungenschaften, auf die ewig niemand gekommen ist, die wir heute jedoch als selbstverständlich ansehen.

——————————

In der Mathematik ist es übrigens fast immer so, dass man generell auf neue Begriffe verzichten könnte und alles mit den alten Begriffen ausdrücken könnte, z.B. könnte man auf die Einführung negativer Zahlen verzichten und alles mit den natürlichen Zahlen ausdrücken, statt zu sagen: Man besitzt −1000€−1000€ könnte man ja auch einfach sagen, dass man 1000€1000€ Schulden besitzt! Irgendwann jedoch würde es immer komplizierter werden alles mit den alten Begriffen auszudrücken und neue Begriffe drängen sich mehr und mehr auf. Das Fehlen neuer Begriffe kann sogar zu einer Behinderung des Fortschritts eines Wissenschaftsgebietes führen, da es sehr schwer wird, sich in das Gebiet einzuarbeiten und es auch immer umständlicher wird mit den alten Begriffen zu operieren.