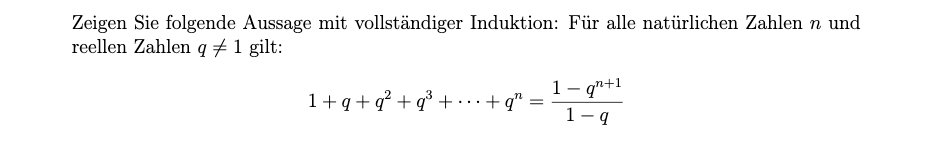Hallo, das machst Du wie immer. Induktionsanfang: n=1, q=2. Gibt dann \(1+2=\frac{1-2^2}{1-2}= \frac{-3}{-1}\), also auch 3, passt Jetzt n durch k ersetzen.\(...q^k = \frac{1-q^{k+1}}{1-q}\). Nun k+1 dazu addieren. \(...q^k+q^{k+1} = \frac{1-q^{k+1}}{1-q}+q^{k+1}\) Hauptnenner: \(\frac{1-q^{k+1}+(1-q)*q^{k+1}}{1-q}\) Kürzen: \(\frac{1-q*q^{k+1}}{1-q}= \frac{1-q^{k+2}}{1-q}\). Nun bei der Behauptung n durch k+1 ersetzen und schauen, ob das gleiche rauskommt. \(\frac{1-q^{(k+1)+1}}{1-q}\) Stimmt, fertig. Gruß jobe